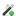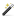Деформации плотины и основания

В формировании напряженного состояния на контакте плотины и ее основания существенную роль играет различие в де­формациях собственно плотины в подошвенном ее сечении и деформациях осно­вания, возникающих под нагрузкой от плотины. Рассмотрим эти деформации на примере, приводимом Ф. Тёльке.
Плотина треугольного профиля (рис. 8.21), высотой 60 м, шириной по низу 43,8 м (m=0,73), с удельным весом бетона =2,3104 Н/м³, модулем  упругости

 Рис. 8.21 Смещение  граней   и подошвы плотины (h=60 м):
a - при наполненном водохранилище; б – при опорожнении

 
Рис. 8.22 Схемы деформаций поверхности ска­лы под действием:
а - треугольной нагрузки от плотины;   б - давления воды на дно верхнего бьефа

 его E_б=20 ГПа. Деформации ее (смещение точек) от давления воды верхнего бьефа и собственного веса, исчисленные для гребня и подошвенного сечения, по­казаны на рис. 8,21, а в искаженном масштабе (в мм); деформации ее же только от собственного веса показаны на рис. 8.21, б. Из рисунка видно, что при напол­ненном водохранилище гребень плотины отклонится в сторону нижнего бьефа на 6,07 мм, или на 0,01% от высоты. Подошвенное сечение как бы прогнется на величину до 0,48 мм, причем напорная грань по этому сечению сдвинется на 1,17 мм. В случае опорожненного водохранилища напорная грань деформируется в сторону верхнего бьефа (гребень на 2,84 мм с одновременным его понижением на 2,07 мм).

Деформации основания происходят под действием нагрузки, передаваемой ему плотиной, и веса воды, заполняющей верхний бьеф.

Нагрузка от плотины счи­тается «гибкой», по эпюре         в) напряжений в подошвенном  шве (рис. 8.22 - ,  или суммарно р), нагрузка от воды верхнего бьефа равно­мерно распределена.

Характер деформаций основания, подсчитанных исходя из теории Буссинеска о напряженном состоя­нии полуплоскости под дей­ствием сосредоточенной и полосовой нагрузки, пока­зан на рис. 8.22 (и - гори­зонтальные, v- вертикаль­ные смещения). В первом случае основание под пло­тиной оседает, а во втором, наоборот, выпучивается.

Для указанного выше примера плотины высотой 60 м Ф. Тёльке просчитал смещения основания в разных случаях нагружения в предположении, что модуль деформации основания Е0 тот же, что и у плотины (Е_n=Е₀). На рис. 8.23 пока­заны эти смещения (в виде кривых). Из сопоставления кривой 2 и данных рис. 8.21, б видно, что смещение поверхности основания значительно больше, чем смещение точек подошвы плотины, основание должно «оторваться» от по­дошвы; сопоставления кривой 4 - суммарной деформации основания и рис. 8.21, а (деформация подошвы плотины) также различны как по вертикали, так и по горизонтали. Если же модуль деформации основания Е0 будет отличаться от модуля упругости плотины Е_п, то расхождения в деформациях подошвы пло­тины и поверхности основания оказываются еще большими.

Поскольку плотина и основание связаны между собой (сила сцепления, тре­ние), обеспечение монолитности контакта их возможно лишь приложением допол­нительных внутренних напряжений на контакте, что меняет существенно общую картину напряжений плотины и основания, исчисленных методом теории упруго­сти (или тем более методом сопротивления материалов); в частности, линейное распределение напряжений превращается в криволинейное.

Понравилось? Поделитесь материалом