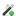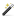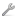Поперечные профили плотин. Исходный поперечный профиль плотины

Первые по времени плотины, например, Пуэнтес (1791), Гробуа (1838) имели тяжелые поперечные профили (рис. 8.1), близкие к трапеции или даже к прямоугольнику. Но в дальнейшем с разработкой теории расчета появились более экономичные профили плотин криволинейного или полигонального очертания. Однако наиболее экономичным оказал­ся профиль, в основе своей представляющий треугольник с некоторыми отклонениями и коррективами       вызванными условиями работы плотины. В настоящее время в большинстве случаев грави­тационные бетонные плотины проектируются треугольного профиля.  ­

Статический расчет гравитационных плотин обычно ведут рассматривая лишь силы, действующие в плоских сечениях, нормаль­ных к оси плотины, т. е. в условиях плоской   задачи. Рассмотрим участок плотины единичной длины (1м) сечением в виде треугольника АВС (рис. 8.2) с основанием b, высотой h и наклоном сторон - заложением напорной грани пb и низовой (1-пb)b где . На плотину  действуют следующие силы: собственный вес сооружения G, давление воды  верхнего бьефа    с горизонтальной составляющей W₁, и   вертикальной W₂; фильтрационное   давление W_ф с эпюрой в виде  треугольника высотой а₁h - давление воды со стороны нижнего бьефа принято равным нулю. Верхний бьеф

Рис. 8.1 Профили некоторых гравитационных плотин:
а - глухие;   1 - Гробуа   (1838);   2 - Пуентес   (1791);   3 - Фюранс   (1866);   4 - Шамбон   (1936); 5 - Братская (1965); 6 - Гренд-Кули  (1942); 7 - Токтогульская  (строится); 8 - Гувер   (1935);   9 - Гранд Диксанс    (1961);    б - водосливные;    1 - Цимлянская   (1951); 2 - Днепровская   им.   Ленина   (1932);   3 - Норис   (1935);   4 - Гренд-Кули   (1942);   5 - Красноярская (1970); 6 - Шаста (1944)

 
Рис. 8.2 Схема сил и напряжений в плотине треугольного профиля

предполагается наполненным водой на всю высотуh. Задача ана­лиза заключается в нахождении экономичного по размерам и фор­ме сечения, характеризуемого минимальной шириной понизу при заданной высоте.

Нормальные краевые напряжения    в горизонтальных сечениях профиля можно определить по формуле неравномерного сжатия

          (8.1)

где V - сумма вертикальных сил, нормальных к основанию;

V=G+W₂ -W_ф; М - момент всех сил относительно центра тяжести (середины) сечения.

При принятых выше обозначениях сила

           (8.2)

где и  - удельные веса воды и тела плотины (бетон):

 (8.3)

 Нормальное напряжение на напорной грани оУ (при напол­ненном водой верхнем бьефе) получим, подставив в формулу (8.1) величины Vи М из формул (8.2) и (8.3), взяв знак минус перед вторым членом формулы (8.1) и произведя необходимые алгебраи­ческие преобразования

          (8.4)

 Учитывая   что     нормальное напряжение на низовой грани  найдем, пользуясь формулой (8.4)

              (8.5)

 Для случая отсутствия воды в верхнем бьефе (строительный пе­риод или опорожненное водохранилище) нормальные краевые на­пряжения в основании плотины можно получить из формул (8.4) и (8.5), приняв в них

                    (8.6)

                                (8.7)

 Силу W_ф в приведенных выше выражениях следует понимать двояко:

1) если бетон плотины проницаем для воды и плотина фильтрует с образованием в ней поверхности (кривой) депрессии, за которую можно принять прямую аb (см. рис. 3.35) или приближенно низовую грань плотины АС (рис. 8.2), то сила W_ф есть Архимедова сила взвешивания бетона, коэффициент а учитывает в этом случае пористость бетона, равную , а  ;

2) если плотина не фильтрует, но основание ее водопроницае­мо, то W_ф представляет собой фильтрационное противодавление на подошву плотины АВ и , где  - коэффициент уменьшения давления за счет сопротивления движению воды в по­рах и трещинах основания и различных мероприятий, как завеса и дренажи (см. § 3.5). Величина  может быть равна , но может быть и обычно меньше .

Понравилось? Поделитесь материалом