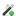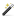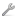Расчет напряжений в плотине от действия сосредоточенной силы, при­ложенной в вершине профиля

Эта задача была решена Митчелем в полярных координатах с началом их О в вершине треугольного профиля (рис. 8.16). Ось полярных координат ОС проходит по биссектрисе угла и углы лучей  отсчитываются от этой оси. К оси прямоугольных координат ОYось ОG наклоне­на под углом .

Напряжение от силы R, приложенной в вершине профиля О, на элементарной площадке в точке Dна луче OD обозначим  в радиальном направлении и в тангенциальном направлении.

На практике приходится определять напряжения отдельно от вертикальной Р и горизонтальной Qсоставляющих силы R (рис. 8.16).

 Рис. 8.16 Схема к расчету напряжений   от    сосредото­ченной силы и момента

Напряжения, вызванные силой Р, равны:

     (8.48)

 а силой Q.

    (8.49)

где

      (8.50)

 В выражениях (8.48) и (8.49) величина , где - угол, состав­ленный лучом ОDс осью у прямоугольных координат, а х и у - координаты рассматриваемой точки D для которой определяются напряжения .

По напряжению определяются напряжения в точке D в системе прямо­угольных координат

         (8.51)

Понравилось? Поделитесь материалом